Tag: مساله روز تولد

حل مسأله‌ی روز تولد به کمک زنجیره‌ی مارکوف

آذر. ۰۲ آموزش‌های دانشگاهی یک دیدگاه

طبق وعده‌ی پیشین قرار بود مهلت آخر ارسال جواب‌ها دیشب باشد و البته یک روز هم مهلت اضافی درنظر گرفته شد تا دوستانی که اظهار تمایل و علاقه به حل این مسأله داشتند فرصت کافی برای ارسال جولب داشته باشند که تعدادی از دانشجویان نیز جواب را ارسال کرده اند

image

اما بعد:
اولا برای دریافت فایل PDF جواب مفصل این سوال حتما اینجا را کیک کنید.

همانطور که در متن مساله (این پست را ببینید) اشاره کرده بودم برای حل این مسأله باید سیستمی را در نظر می‌گرفتیم که داراری ۸ حالت است و گذار بین حالت‌ها مطابق با آنچه که در کلاس نیز شرح دادم به صورت زیر است:

image

در این سیستم، زمانی که در وضعیت k هستیم بدان معنی است که روز تولد افراد مورد بررسی k روز هفته را تشکیل داده است. به این ترتیب ماتریس احتمالات گذار بین حالت‌ها قابل محاسبه است

image

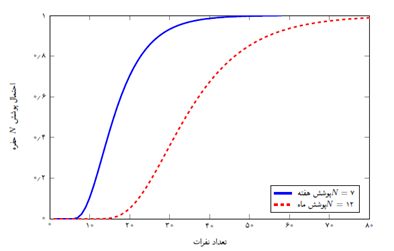
به این ترتیب وقتی که n بار روی این زنجیره – با شروع از صفر- حرکت کنیم. آرایه ردیف ۰ و ستون ۷ نشان دهنده آن است که چقدر احتمال دارد روزهای تولد n نفر هفت روز هفته را پوشش دهد (چرا؟؟؟؟).  بنابراین جواب مسأله عبارت خواهد بود از یافتن nای که

image

اما چگونه این n را بیابیم؟؟؟؟؟؟؟؟؟

۱- روش ضرب متوالی ماتریس‌ها: که قریب به اتفاق جواب‌ها از این کلک رشتی؟؟؟ استفاده کرده‌اند و جواب را پیدا کرده‌اند. بنابراین به این بخش از دوستان نیز نمره‌ای تعلق خواهد گرفت. توضیح آن در متن هست

۲- روش تجزیه ماتریس

image

image

image

image

و خوب مابقی جواب مشخص است. این راه حل هم به عنوان مثال با استفاده از دو دستور محاسبه مقدار ویژه و محاسبه معکوس ماتریس قابل محاسبه است. دوستانی که به این راه حل رسیده باشند نسبت به دوستان ردیف اول نمره بیشتری کسب خواهند کرد

 

۳- راه حل عام: اگر کسی به هر نحوی راه حل عمومی برای این مسأله از طریق تعمیم راه حل ۲ به دست آورده باشد نمره کامل را خواهد گرفت. من راه حل عمومی را در متن پاسخنامه مفصلی که به پیوست این پست قرار داده ام آورده‌ام. لازم است دوستان با عنایت مخصوص راه حل را بخوانند.

 

روش تجزیه ماتریس:

‏ ‎از‎ آنجاییکه ماتریس \mathbf{P}‎ یک ماتریس مربع ‎n‎\times ‎n‎‎‎‏ است‏، دارای ‎‎‎‎n‎‎‏ مقدار ویژه ‎‎‎‎‎\lambda‎_1,‎\lambda‎_2,‎\ldots‎,‎\lambda‎_n‎‎‏ است. فرض می‌کنیم که این مقادیر ویژه منفرد (غیرتکراری) و غیر صفر هستند. فرض منفرد بودن مقادیر ویژه ماتریس احتمالات گذار در بسیاری از کاربردهای عملی برقرار است (به غیر از مواردی که زنجیره مارکوف کاهش پذیر و تناوبی است که در این حالت نیز با تغییراتی بحث‌های آتی برقرار است). علاوه بر این مقدار ویژه صفر نیز ممکن است در میان مقادیر ویژه باشد که فعلا این حالت را نیز در نظر نمی‌گیریم\cite{Papoulis1991}. با این مقدمات فرض کنید ‎‏که جفت‌های ‎‎‎‎(‎\lambda‎_‎i,‎‎\mathbf{u}‎_i)‎\;\; ‎i=1,2,‎\ldots‎,n‎ ‎‎‏‎‎‎n‎‎‎‎‎‎‎‎‎‏ زوج مقدار- بردار ویژه ماتریس ‎‎‎‎\mathbf{P}‎‎‏ باشند. داریم:
‎

(۱)   \begin{equation*} ‎\mathbf{P}‎\mathbf{u}_i=‎\lambda‎_i ‎\mathbf{u}‎_i\;\;\;\;\; i=1‎\rightarrow ‎n‎ \end{equation*}

یا
‎

(۲)   \begin{equation*} ‎\mathbf{P}‎‎\mathbf{U}‎‎=‎\mathbf{U}‎‎‎\Lambda‎ \end{equation*}

‎‏‎
که در آن ماتریس‎‏‌های مربعی ‎‎‎‎‎\mathbf{U}‎‎‎‏ و‎‎‏ ‎‎‎‎\Lambda‎‎‏ به صورت زیر تعریف می‌شوند:
‎

(۳)   \begin{equation*} ‎‎\mathbf{U}‎‎=\left[‎\mathbf{u}‎_1,‎\mathbf{u}‎_2,\ldots‎,‎\mathbf{u}‎_n\right] \end{equation*}

‎
‏ و
‎

(۴)   \begin{equation*} \Lambda=\begin{pmatrix} ‎‎\lambda‎_1 & &‎ & ‎‎‎0 ‎\\‎‎ & ‎\lambda‎_2 & & \\‎ & & ‎\ddots &‎ ‎\\‎ 0 &‎ &‎ & ‎‎‎‎\lambda‎_n‎ \end{pmatrix} \end{equation*}

از آنجا که ‎‎‎‎‎\mathbf{u}‎_i‎‎‎‏ها بردارهای ستونی ‎n \times ‎1‎‎‎‏ و مستقل خطی هستند‏،‏ ماتریس ‎‎‎‎‎\mathbf{U}‎_{n\times ‎n‎}‎‎‏ ‏ یک ماتریس غیرمنفرد و دارای وارون است و داریم:
‎

(۵)   \begin{equation*}‎‎ ‎\mathbf{P}‎=‎\mathbf{U}‎‎{\Lambda}‎‎\mathbf{U}‎^{-1}=‎\mathbf{U}‎‎{\Lambda}‎‎\mathbf{V} \end{equation*}

‎‎‏‎
که:
‎

(۶)   \begin{equation*} ‎\mathbf{V}‎‎\mathbf{P}‎=‎‎{\Lambda}‎‎\mathbf{V} \end{equation*}

که:
‎

(۷)   \begin{equation*} ‎\mathbf{V}‎‎=‎‎\mathbf{U}‎^{-1}=‎\left[‎‎‎ \begin{array}{c} ‎\mathbf{v}‎_1\\‎ \mathbf{v}‎_2\\‎‎ ‎\vdots ‎\\‎ \mathbf{v}‎_n‎‎ \end{array} \right] \end{equation*}

‎
‏ که در آن ‎‎‎‎‎\mathbf{v}‎_k‎‎‏ نشان‌دهنده‌ی ‎‎‎‎k‎‎‎‏امین بردار سطری از ماتریس ‎‎‎‎‎\mathbf{V}‎‎‎‏ است و ‎‎‎‎\mathbf{V}\mathbf{U}=1‎‎‏ (یا ‎‎‎‎v_k‎ u_k=1\;\;\;‎‎‎v_‎i‎ u_k=0\;\; i\neq k ‎‎‏) است. ‏از معادله‌ی ‎‎۵‎‎‏ به دست می‌آوریم که:
‎

(۸)   \begin{equation*} ‎\mathbf{P}‎^n=‎\mathbf{U}‎‎\Lambda‎^{n}‎\mathbf{V}‎=\sum_{k=1}^{n}‎\lambda‎_k^n‎ \mathbf{u}‎_k‎\mathbf{v}‎_k \end{equation*}

‏ و یا:
‎

(۹)   \begin{equation*} ‎‎p_{i,j}‎‎^{(n)}=‎‎‎‎‎\sum_{k=1}^{n}‎\lambda‎_k^n ‎u_{ik}‎‎‎‎v_{kj} \end{equation*}

‎
‏ به بیان ساده‌تر معادلات بالا بیان‌کننده این هستند که به ازای هر یک از مقادیر ویژه ماتریس ‎‎‎‎\mathbf{P}‎‎‏ نظیر ‎‎‎‎‎\lambda‎_k , k=1,‎\ldots‎,n‎‎‏ بردارهای ‎‎‎‎u_k‎‎‏ و ‎‎‎‎v_k‎‎‏ مجموعه معادلات زیر را ارضا می‌کنند
‎

(۱۰)   \begin{equation*}‎‎ \sum_{i=1}^n p_{i,j}x_j^{(k)}=‎\lambda‎_k x_i^{(k)} \end{equation*}

‎

(۱۱)   \begin{equation*}‎‎ \sum_{i=1}^n y_i^{(k)}p_{i,j}=‎\lambda‎_k y_j^{(k)} \end{equation*}

‎
‏ به این ترتیب می‌توان الگوریتمی برای محاسبه مستقیم ‎‎‎‎p_{i,j}^{(n)}‎‎‏ به دست آورد:
‎\begin{enumerate}
‎\item‎‎
‏ ‎ابتدا‎ مقادیر ویژه ماتریس احتمالات گذار از حل معادله ‎\mathrm{‎det}(‎‎‎‎‎\mathbf{P}-‎\lambda‎‎\mathbf{I})‎‎=0‎‎‏ به دست می‌آیند.‎
‎\item‎‎
‏ ‎برای‎ هر یک از مقادیر ویژه ‎‎‎‎‎\lambda‎_k‎‎‏ با استفاده از معادلات ‎‎۱۰ ‎‎‏ و ‎‎‏ ۱۱‎‎ بردارهای ‎‎‎‎\{x_i^{(k)}\}‎‎‏ و ‎‎‎‎\{y_i^{(k)}\}‎‎‏ محاسبه می‌شوند. ضمناً چون بردارهای ‎‎‎‎‎\mathbf{U}‎‎‎‏ و ‎‎‎‎‎\mathbf{V}‎‎‎‏ وارون یکدیگر هستند مقدار ضریب نرمال‌کننده از رابطه‌ی زیر محاسبه می‌شود
‎

(۱۲)   \begin{equation*}\nonumber ‎\mathbf{v}‎_k‎\mathbf{u}‎_k=c_k\sum_{i=1}^{n}x_i^{(k)}y_i^{(k)}=1 \end{equation*}

‎
‏ ‎یا:
‎ ‎

(۱۳)   \begin{equation*}‎‎‎‎ ‎c_k=‎‎\frac{1}{\sum_{i=1}^{n}x_i^{(k)}y_i^{(k)}} \end{equation*}

‎‎‏‎
‎‎\item‎‎‏‎
در نهایت بر حسب مقادیر ‎‎‎‎c_k‎‎‎‏‏، ‎‎‎‎\mathbf{x}‎^{(k)}‎‎‎‎‏ و ‎‎‎‎\mathbf{‎y‎}‎^{(k)}‎ ‎‎‏احتمال‎‎ گذار از ‎‎‎‎i‎‎‏ به ‎‎‎‎j‎‎‏ با ‎‎‎‎n‎‎‎‏گام از طریق رابطه‌ی زیر محاسبه می‌شود:
‎

(۱۴)   \begin{equation*}‎‎ p_{i,j}^{(n)}=\sum_{k=1}^{n}c_k‎\lambda‎_k^n x_i^{(k)}y_j^{(k)} \end{equation*}

\end{enumerate}‎

حل مساله

‏ ‎برای‎ حل مسأله در حالت کلی‏، اجازه بدهید که آن را به این صورت بازطرح کنیم. فرض کنید ‎‎‎‎N‎‎‏ سبد خالی وجود دارد. در هر مرحله به تصادف توپی در یکی از این سبدها انداخته می‌شود. احتمال افتادن توپ به هر یک از این سبدها برابر است و به محتوای سبدها ربطی ندارد. ظرفیت سبدها نیز در این احتمال بی‌تأثیر است. فرض کنید ‎‎‎‎n‎‎‏ توپ به این روش درون سبدها انداخته شده است. احتمال این‌که ‎‎‎‎m‎‎‏ سبد از مجموعه‌ی سبدها خالی و فاقد هر توپی باشد چقدر است؟

مطابق آنچه که در بخش اول گفتیم‏، می‌توان این مسأله را به محاسبه‌ی یک احتمال در زنجیره مارکوف سیستمی تحویل کرد که متشکل از ‎‎‎‎N+1‎‎‏ حالت است. در این سیستم‏، اگر در وضعیت ‎‎‎‎k‎‎‏ باشیم بدان معنی است که ‎‎‎‎k‎‎‏ تا از سبدها دارای توپ و ‎‎N‎-k‎‎‎‏تا از سبدها فاقد توپ است.

‎اگر ‎‎‎‎n‎‎‏ توپ درون سبدها انداخته شده باشد‏، احتمال اینکه ‎‎m‎ ‎‏سبد‎ خالی باشد برابر است با ‎‎‎‎p_{0,N-m}^{(n)}‎‎‎‏.‏ برای محاسبه‌ی این احتمال لازم است توان ‎‎‎‎n‎‎‎‏ام ماتریس را به شکل صریح محاسبه کنیم. برای این منظور از الگوریتم بخش قبلی استفاده می‌کنیم.

مطابق با آنچه در این زنجیره مشاهده می‌شود‏، ‎‎‎‎p_{i,i}=‎\frac{i}{N}‎‎‎‏ و ‎‎‎p_{i,i+1}=‎\frac{‎N-‎i}{N}‎‎ ‎‎‏ به این ترتیب معادله~‎‎۱۰‎‎‏ مربوط به محاسبه ‎‎‎‎x_i‎‎‎‏ها به رابطه‌ی زیر تقلیل می‌یابد:
‎

(۱۵)   \begin{equation*}‎‎‎‎ (N‎\lambda‎_k-i)x_i^{(k)}=(N-i)x_{i+1}^{(k)} \end{equation*}

‎
‏
در حالت ‎‎‎‎‎\lambda‎_k=1‎‎‏ مقدار ‎‎‎‎x_i‎‎‏ برای تمام ‎‎‎‎i‎‎‎‏ها برابر با ۱ خواهد بود. ضمناً در حالت ‎‎‎‎‎\lambda‎_k‎\neq ‎1‎‏‎‎ به‌ازای ‎‎‎‎i=N‎‎‏ مقدار ‎‎‎‎x_N=0‎‎‏ به دست می‌آید و با جایگذاری مستقیم در رابطه‌ی بالا به ازای ‎‎‎‎i=N-1‎‎‏ نیز مقدار ‎‎‎‎x_{N-1}=0‎‎‏ به دست می‌آید و به همین ترتیب تا پایان. اما مقادیر بردارهای ویژه همگی نمی‌توانند صفر باشند. بنابراین باید ‎‎‎‎k‎‎‎‏ای وجود داشته باشد که ‎‎‎‎x_{k+1}=0‎‎‏ باشد اما ‎‎‎‎x_{k}\neq0‎‎‏. در این حالت ‎‏از معادله‌ی ‎~‎۱۵‎‎ به دست می‌آید که:‏ ‎‎‎‎N‎\lambda‎_k-k=0‎‎‏ و لذا مقادیر ویژه عبارت خواهند بود از:
‎

(۱۶)   \begin{equation*} \lambda_k=‎\frac{k}{N}‎\;\;\;\;\; k=1,2,‎\ldots‎,N \end{equation*}

‎
‏ با این مقدار ویژه معادله‌ی ‎~‎۱۵‎‎ به صورت زیر تبدیل خواهد شد:
‎

(۱۷)   \begin{equation*}‎\nonumber‎‎‎ (k-i)x_i^{(k)}=(N-i)x_{i+1}^{(k)}\;\;\;\; i\leq k \end{equation*}

‎
‏از حل این معادله‌ی بازگشتی داریم:

(۱۸)   \begin{equation*} ‎‎‎‎ \begin{split}‎‎ x_i^{(k)}=‎\frac{(k-i+1)}{(N-i+1)}‎x_{i-1}^{(k)}&=‎\frac{(N-i)!}{N!}‎‎\frac{k!}{(k-i)!}\\‎‎ &=‎\left\lbrace ‎‎ \begin{array}{ll}‎ ‎\dfrac{\binom{k}{i}}{\binom{N}{i}} &‎ ‎i\leq k‎ ‎\\‎‎ & \\ 0‎ &‎ ‎i>k‎ \end{array} \right.‎ \end{split} \end{equation*}

به روشی مشابه و با حل معادله‌ی‎~‎۱۱‎‎‏ به ازای‎‎‏ ‎‎‎‎‎\lambda‎_k=‎\frac{k}{N}‎‎‎‏ داریم:
‎

(۱۹)   \begin{equation*} y_{j-1}^{(k)}p_{j-1,j}+ y_{j}^{(k)}p_{j,j}=‎\lambda‎_k y_{j}^{(k)} \end{equation*}

‎
‏ یا:
‎

(۲۰)   \begin{equation*}\nonumber ‎(k-j)‎y_{j}^{(k)}=(N-j+1) y_{j-1}^{(k)} \end{equation*}

‎‎
‏ که در نتیجه‎‎‎‎y_{k-1}^{(k)}=0‎‎‏ و
‎

(۲۱)   \begin{equation*}‎‎‎‎ y_{j}^{(k)}=‎\left\lbrace ‎‎ \begin{array}{ll}‎ 0 & j & \\ (-1)^{j-k}\binom{N-k}{j-k} & j \geq k \end{array}‎ \right.‎ \end{equation*}

‎
‏اما‏، برای محاسبه‌ی ضرایب نرمال‌کننده ‎‎‎‎c_k‎‎‏ (چون ‎‎‎‎‎\mathbf{‎U‎}=\mathbf{V‎}^{-1}‎‎‎‎‏‎‏) به این نکته توجه می‌کنیم که برای ‎‎‎‎i>k‎‎‏ مقدار ‎‎‎‎x_i^{k}=0‎‎‏ و برای ‎‎i<k‎‎‎‎‎‏ مقدار=”” ‎‎‎‎y_{i}^{(k)}="0‎‎‏” است=”” و=”” در=”” نتیجه‏=”” از=”” معادله‌ی=”” ‎~‎۱۳‎‎‏=”” داریم=”” ‎‎‎‎c_k="\binom{‎‏‎N‎}{k}‎‎‏” ‎‏‎<="" p="">

با جایگذاری مقادیر روابط ‎~‎۲۱‎‎‏ و ‎~‎۱۸‎‎‏ در رابطه‌ی ‎~‎۱۴‎‎‏ داریم:
‎

(۲۲)   \begin{equation*}‎‎‎‎ \begin{split}‎‎ p_{ij}^{(n)}&=\sum_{k=i}^{j}{‎\lambda‎_k^{n}c_kx_i^{(k)}y_j^{(k)}} \\‎ &=\sum_{k=i}^{j}{‎‎\left(‎‎‎\dfrac{k}{N}‎\right)‎^{n}‎‎{(-1)}^{j-k}\binom{N}{k}\binom{k}{i}\binom{N-k}{j-k}\Big /\binom{N}{i}}‎\\‎ &=\sum_{k=i}^{j}{‎‎\left(‎‎‎\dfrac{k}{N}‎\right)‎^{n}‎\frac{(N-i)!}{(N-j)!}‎\frac{(-1)^{j-k}}{(j-k)! (k-i)!}} \\‎ &=\binom{N-i}{N-j}\sum_{k=i}^{j}{(-1)^{j-k}‎‎\left(‎‎‎\dfrac{k}{N}‎\right)‎^{n}\binom{j-i}{k-i}}\\‎ &=\binom{N-i}{N-j}\sum_{r=0}^{j-i}{(-1)^{j-i-r}‎‎\left(‎‎‎\dfrac{r+i}{N}‎\right)‎^{n}\binom{j-i}{r}} \;\;\; j\geq i\\‎ \end{split} \end{equation*}

‎
‏ می‌دانیم که‏ برای ‎‎‎‎j<i‎‎‏ داریم:=”” ‎‎‎‎p_{ij}^{(n)}="0‎‎

بر‎ اساس رابطه‌ی ‎~‎۲۲‎‎‏ در حالت خاص و برای ‎‎‎‎i=0‎‎‏ ( حالت شروع) معادله‌ی ‎‎۲۲‎‎‏ به رابطه‌ی‌‎۲۳‎ کاهش می‌یابد
‎

(۲۳)   \begin{equation*}‎‎ p_{0,j}^{(n)}=\binom{N}{N-j}\sum_{r=0}^{j}{‎‎\left(‎‎‎\dfrac{r}{N}‎\right)‎^{n}\binom{j}{r}(-1)^{j-r}} \end{equation*}

‏ رابطه‌ی‎‎۲۳‎‎‏ احتمال پر بودن ‎‎‎‎j‎‎‏ سبد بعد از پرتاپ تصادفی ‎‎‎‎n‎‎‏ توپ بین ‎‎‎‎N‎‎‏ سبد (یا خالی بودن ‎‎‎‎N-j‎‎‏ سبد) را نشان می‌دهد. از این رابطه می‌توانیم برای پاسخگویی به احتمال خواسته شده در مسأله استفاده کنیم.

فرض کنید ‎‎‎‎m=N-j‎‎‏ تعداد سبدهای خالی در مرحله‌ی ‎‎‎‎n‎‎‏ را نشان دهد. متغیر جدید ‎‎‎‎v=N-m-r‎‎‏ را تعریف می‌کنیم به‌گونه‌ای که:
‎

(۲۴)   \begin{equation*}‎‎‎‎ \begin{split}‎‎ p_{0,j}^{(n)}&=\binom{N}{m}\sum_{v=0}^{N-m}{{(-1)}^v\binom{N-m}{v}{‎\left(‎‎1-‎\dfrac{m+v}{N}‎\right)‎}^{n}} \\‎ &=‎\frac{1}{m!}‎\sum_{v=0}^{N-m}{‎\frac{{(-1)}^v}{v!}‎‎\frac{N!}{(N-m-v)!}‎\left(‎‎1-‎\dfrac{m+v}{N}‎\right)‎^{n}‎} \end{split} \end{equation*}

‎
‏برای محاسبه‌ی حالت حدی‏ ‏زمانی‌که ‎‎‎‎n\rightarrow \infty‎‎‏ و ‎‎‎‎N\rightarrow \infty‎‎‏ در رابطه‌ی ‎‎۲۴‎‎‏ داریم:
‎

(۲۵)   \begin{equation*} ‎\frac{N!}{(N-m-v)!}‎=‎\prod‎_{k=0}^{m+v-1}(N-k)=N^{m+v}‎\prod‎_{k=0}^{m+v-1}(1-‎\frac{k}{N}‎)‎\rightarrow ‎N^{m+v}‎ \end{equation*}

‎
‏و
‎

(۲۶)   \begin{equation*} ‎\left(1-‎\frac{m+v}{N}‎ ‎\right)‎^{n}‎\rightarrow ‎e^{-(m+v)n/N}‎ \end{equation*}

و با جایگذاری این دو در رابطه‌ی‎‎۲۴‎‎‏ داریم:
‎

(۲۷)   \begin{equation*}‎‎ \begin{split}‎‎ ‎\lim‎_{N,n‎\rightarrow ‎\infty}{p_{0,N-m}^{(n)}}&=\lim_{N,n‎\rightarrow ‎‎\infty‎}‎\frac{1}{m!}\sum_{v=0}^{N-m}{‎\frac{(-1)^v}{v!}‎‎‎N^{m+v}e^{-(m+v)n/N}}‎\\‎ &=\frac{(Ne^{-n/N})^m}{m!} \sum_{v=0}^{\infty}‎\frac{(-Ne^{-n/N})^v}{v!}‎\\‎ &=‎\frac{\lambda^m}{m!}‎e^{-‎\lambda‎} \end{split} \end{equation*}

‎
‏که:
‎

(۲۸)   \begin{equation*}‎‎‎‎ ‎\lambda‎=N e^{-n/N} \end{equation*}

‎
‏بر اساس این رابطه‏، اگر ‎‎‎‎n‎‎‎‏و ‎‎‎‎N‎‎‏ به‌گونه‌ای تغییر یابند که ‎‎‎‎‎\lambda‎‎‎‏ محدود باقی‌ بماند‏، احتمال خالی ماندن ‎‎‎‎m‎‎‏ سبد‏، زمانیکه ‎‎‎‎n‎‎‏ توپ میان ‎‎‎‎N‎‎‏ سبد (بدواً خالی) به صورت تصادفی توزیع می‌شود از توزیع پوآسون‎‎۲۷‎‎ تبعیت می‌کند.‏ به این ترتیب مثلاً احتمال اینکه روز تولد یک جمعیت ۲۰۰۰ نفری تمام ۳۶۵ روز یک سال را پوشش دهد برابر است با ‎‎‎‎e^{-‎\lambda‎}=e^{-1.5226}=0.2181‎‎‏ (با قرار دادن ‎‎‎‎m=0‎‎‏ در ‎‎۲۷‎‎‏ و ‎‏محاسبه‎‎‎‎‏‌ی ‎‎‎‎‎\lambda‎‎‎‏ بر اساس رابطه‌ی‎‎۲۸‎‎‏ ‎‎‎‎\lambda=365e^{-2000/365}=1.5226‎‎‏ )

حال‎‎ با این مقدمه‌ی نسبتاً مفصل برگردیم به مسأله‌ی خودمان؛ برای محاسبه‌ی این که حداقل چند نفر باید در یک‌جا جمع باشند تا با احتمال بیش از ۹۵٪ روز تولد آنها تمام روزهای هفته را بپوشاند بایستی مقدار ‎‎‎‎n‎‎‎‏ای را محاسبه کنیم که به ازای آن ‎‎‎‎p_{0,7}^{(n)}\geq 0.95‎‎‏ باشد. به این ترتیب داریم:
‎

(۲۹)   \begin{equation*}‎ \begin{split} &‎‎‎p_{0,7}^{(n)}=‎‎‎e^{-‎\lambda‎} \geq 0.95 ‎\Rightarrow ‎‎\lambda‎=-\ln‎(0.95)=0.0513‎\\‎ &‎‎\lambda‎=N e^{-n/N} ‎\Rightarrow ‎\ln(‎\lambda‎)=\ln(N)-‎\frac{n}{N}‎‎‎\Rightarrow ‎n=N\ln(N)+N\ln(1/‎\lambda‎)=N\ln(‎\frac{N}{‎\lambda‎}‎‎‎)\\ &n=7\ln(‎\frac{7}{‎0.0513})= 35 \end{split} \end{equation*}

برچسب‌ها:,

یک تمرین زنجیره مارکوف وسوسه‌انگیز

آبان. ۲۱ روزنوشتهای وبلاگی یک دیدگاه

به قول علما، مسألتاٌ: حداقل چند نفر آدم باید در یک جا جمع باشند تا روز تولد تک تک آنها با یکدیگر و با احتمال بیش از ۹۵٪ همه روزهای هفته را تشکیل دهد

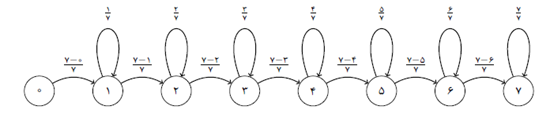
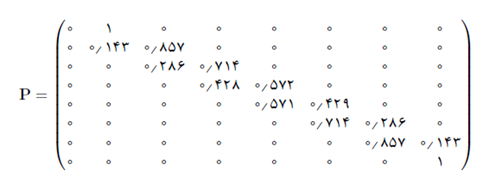
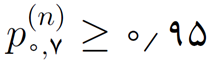
 http://www.beytoote.com/images/stories/fun/fu395.jpgبرای حل این تمرین – که البته مساله مشهوری هم هست در عالم ریاضیات- به کمک زنجیره‌های مارکوف ۱.۵ نمره مازاد امتحانی درنظر گرفته شده است (البته مشروط بر اینکه این جواب تا پایان آبانماه به ایمیل بنده ارسال شده باشد). اما برای حل آن یک راهنمایی هم می‌کنم. فرض کنید n تعداد نفرات مجهولی را نشان دهد که ما به دنبال تعیین آن هستیم. سیستمی را در نظر بگیری که ۸ حالت یا وضعیت دارد (مطابق با ۷ روز هفته از شنبه تا جمعه و یک وضعیت شروع خالی) . به این ترتیب که اگر سیستم در وضعیت k باشد بدان معناست که روزهای تولد جمعیت K روز هفته را تشکیل می‌دهند. بدیهی است که وقتی سیستم در وضعیت k قرار دارد به وضعیت قبلی خود بر نمی‌گردد. با پرسیدن روز تولد نفر بعدی سیستم ممکن است در همان وضعیت باقی بماند و یا ممکن است به وضعیت k+1 برود. احتمال  ماندن در همان وضعیت قطعا k/۷ است و احتمال تغییر وضعیت به k+1 هم که روشن است. سیستم مدنظر از حالت ۰ شروع می‌کند و با احتمال ۱ به حالت ۱ تغییر وضعیت می‌دهد و …… . حال سوال این است که چه توانی از این زنجیره مارکوف تضمیین می‌کند که احتمال حرکت از ۰ به ۷ بزرگتر از ۹۵٪ باشد…… به همین سادگی. فقط یک مشکل وجود دارد و آن هم این است که باید به نحوی توان n ام این ماتریس را محاسبه کرد که از این جا به بعد داستان را دانشجوی علاقمند و صدالبته طالب نمره باید پیدا کند…….. پس منتظر ایمیل‌هایتان هستم

برچسب‌ها:,